Counting Valid Pickup and Delivery Sequences: A Dynamic Programming Approach

1. Introduction

What is the Problem?

You are given n orders, each comprising both pickup and delivery services. The task is to count all the valid sequences of these orders, ensuring that the delivery for each order always occurs after its corresponding pickup. To manage large results, return the count modulo 10^9 + 7.

Constraints:

• 1 <= n <= 500
• Return result modulo 10^9 + 7.
• Pickup must occur before its corresponding delivery.

Why is it Challenging?

Counting valid sequences of pickup and delivery orders while satisfying the constraint that each delivery follows its corresponding pickup can be challenging due to the large number of possible sequences. Dynamic programming is a powerful technique that can be used to optimize the computation of these sequences.

what are mapping techniques for load balancing

2. Dynamic Programming Overview

Dynamic Programming is a powerful technique that involves caching pre-computed results, thereby eliminating the need for redundant computations and significantly optimizing time complexity. There are two primary approaches to Dynamic Programming:

Recursive Approach (Top-Down)

In the Recursive Approach, we break down a complex problem into simpler ones. We calculate the result for n pairs by first calculating the answer for n – 1 pairs, which is easier, and then using its result as part of our solution.

leet Code : Validate Binary Search Tree Java || C++ || C || pYthon

Iterative Approach (Bottom-Up)

The Iterative Approach involves solving simpler problems first and building up to the complex problem. We start by calculating the result for one pair, then for 2, 3, 4, and so on, until we reach n pairs. We build a table of solutions along the way.

3. Understanding the Solution

The intuition behind the Approach

Initially, let’s assume that we don’t require the delivery to occur after its corresponding pickup. We want to find the number of combinations to insert the n-th pair among (n-1) pairs. Imagine having (n-1) * 2 items and inserting two new items anywhere between them.

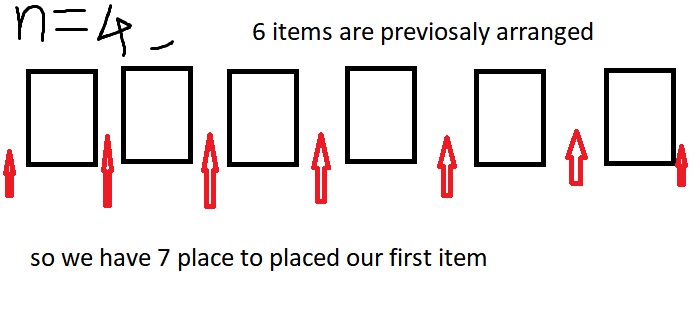
Leet Code : Validate Binary Search Tree Java | CPP | Python solution

For the first item in the n-th pair, we have (n * 2 – 1) new places to insert it. For the second item in the n-th pair, we have (n * 2) places to insert it, considering that we’ve already inserted the first item. So, initially, we have (n * 2 – 1) * n * 2 places to insert our two new items.

Now, considering that we only need the pickup to occur before its corresponding delivery, we divide our formula by two. This gives us (n * 2 – 1) * n ways to insert our n-th pair. We calculate the final solution by multiplying the number of combinations to insert every n-th pair into the (n-1) th pair, starting from 1 and going up to n.

LeetCode: A Quick and Simple Solution to Find the Town Judge

The formula for Counting Valid Sequences

The formula to count valid sequences for n pairs is: (n * 2 – 1) * n

4. Proposed Solutions

Recursive Approach (Top-Down)

Approach:

1. Create a memoization vector to store computed values.
2. Implement a recursive function calculateOrdersCount to calculate the number of valid orders for remainingPairs using recursion and memoization.

• Base case: If remainingPairs is 0, return 1.
• Otherwise, calculate it using the formula (remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD and memoize the result.

1. In the main function countOrders, initialize memoization with -1 values.
2. Call calculateOrdersCount with numPairs to find the count of valid orders.
3. Return the result.

Tackling Jump I , II , III , IV Game Problems on LeetCode | Cpp ,Java ,Python – Day 3

Complexity:

• Time complexity: O(N)
• We calculate the number of combinations for all pairs from n down to 1.
• Space complexity: O(N)
• We store the array used for dynamic programming with size n.

Iterative Approach (Bottom-Up)

Approach:

1. Create a memoization array dp of size numberOfPairs + 1.
2. Set dp[0] to 1 as the base case, representing the one way to arrange 0 pairs.
3. Calculate valid orders iteratively by looping from 1 to numberOfPairs.

• For each value of currentPairs, calculate dp[currentPairs] using the formula: dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD.

1. Return the result.

Complexity:

• Time complexity: O(N)
• We calculate the number of combinations for all pairs from 1 up to n.
• Space complexity: O(N)
• We store the array used for dynamic programming with size n.

5. Code Implementation

Recursive Approach (Top-Down) in C++

class Solution {
public:
    const int MOD = 1e9 + 7;  // Modulus for calculations
    vector<long long> memoization;  // Memoization array to store computed values

    long long calculateOrdersCount(long long remainingPairs) {
        // Base case: No remaining pairs, return 1
        if (remainingPairs == 0)
            return 1;

        // Check if the value is already computed and return it
        if (memoization[remainingPairs] != -1)
            return memoization[remainingPairs];

        // Calculate the number of valid orders for the remaining pairs
        long long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;

        // Store the result in the memoization array and return it
        return memoization[remainingPairs] = currentResult;
    }

    int countOrders(int numPairs) {
        // Initialize the memoization array with -1 values
        memoization.resize(numPairs + 1, -1);

        // Calculate and return the count of valid orders
        return calculateOrdersCount(numPairs);
    }
};

Recursive Approach (Top-Down) in Java

class Solution {
    private int MOD = (int)1e9 + 7;  // Modulus for calculations
    private static final int MAX_PAIRS = 510; // Maximum possible pairs value
    private long[] memoization = new long[MAX_PAIRS];

  // Memoization array to store computed values

    private long calculateOrdersCount(long remainingPairs) {
        // Base case: No remaining pairs, return 1
        if (remainingPairs == 0)
            return 1;

        // Check if the value is already computed and return it
        if (memoization[(int)remainingPairs] != -1)
            return memoization[(int)remainingPairs];

        // Calculate the number of valid orders for the remaining pairs
        long currentResult = calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % MOD;

        // Store the result in the memoization array and return it
        return memoization[(int)remainingPairs] = currentResult;
    }

    public int countOrders(int numPairs) {
        // Initialize the memoization array with -1 values
        for(int i = 0 ; i < numPairs + 5 ; i ++){
            memoization[i] = -1 ;
        }

        // Calculate and return the count of valid orders
        return (int)calculateOrdersCount(numPairs);
    }
}

Recursive Approach (Top-Down) in Python

class Solution:
    def __init__(self):
        self.MOD = int(1e9 + 7)  # Modulus for calculations
        self.memoization = []  # Memoization array to store computed values

    def calculateOrdersCount(self, remainingPairs):
        # Base case: No remaining pairs, return 1
        if remainingPairs == 0:
            return 1

        # Check if the value is already computed and return it
        if self.memoization[remainingPairs] != -1:
            return self.memoization[remainingPairs]

        # Calculate the number of valid orders for the remaining pairs
        currentResult = self.calculateOrdersCount(remainingPairs - 1) * (2 * remainingPairs - 1) * remainingPairs % self.MOD

        # Store the result in the memoization array and return it
        self.memoization[remainingPairs] = currentResult
        return currentResult

    def countOrders(self, numPairs):
        # Initialize the memoization array with -1 values
        self.memoization = [-1] * (numPairs + 1)

        # Calculate and return the count of valid orders
        return self.calculateOrdersCount(numPairs)

Iterative Approach (Bottom-Up) in C++

class Solution {
public:
    const int MOD = 1e9 + 7;  // Modulus for calculations
    vector<long long> dp;    // Array for memoization

    int countOrders(int numberOfPairs) {
        dp.resize(numberOfPairs + 1); // Initialize memoization array

        // Base case: there is one way to arrange 0 pairs
        dp[0] = 1;

        // Iterate over all values of pairs from 1 to n
        for (int currentPairs = 1; currentPairs <= numberOfPairs; currentPairs++) {
            // Calculate the number of valid orders for the current number of pairs
            dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;
        }

        return dp[numberOfPairs]; // Return the result for n pairs
    }
};

Iterative Approach (Bottom-Up) in Java

class Solution {
    private int MOD = (int)1e9 + 7;  // Modulus for calculations

    public int countOrders(int numPairs) {
        // Memoization array to store computed values
        long[] dp = new long[numPairs + 1];

        // Base case: there is one way to arrange 0 pairs
        dp[0] = 1;

        // Iterate over all values of pairs from 1 to n
        for (int currentPairs = 1; currentPairs <= numPairs; currentPairs++) {
            // Calculate the number of valid orders for the current number of pairs
            dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;
        }

        return (int)dp[numPairs]; // Return the result for n pairs
    }
}

Iterative Approach (Bottom-Up) in Python

class Solution:
    def countOrders(self, numPairs: int) -> int:
        MOD = int(1e9 + 7)  # Modulus for calculations
        MAX_PAIRS = numPairs + 1  # Maximum possible pairs value

        # Initialize the memoization array with -1 values
        dp = [0] * MAX_PAIRS

        # Base case: there is one way to arrange 0 pairs
        dp[0] = 1

        # Iterate over all values of pairs from 1 to n
        for currentPairs in range(1, numPairs + 1) :
            # Calculate the number of valid orders for the current number of pairs
            dp[currentPairs] = dp[currentPairs - 1] * (2 * currentPairs - 1) * currentPairs % MOD;

        # Return the result for n pairs
        return dp[numPairs];

6. Conclusion

Counting valid pickup and delivery sequences can be efficiently solved using dynamic programming. The provided solutions offer both recursive and iterative approaches to tackle the problem. These approaches help us handle large values of n while satisfying the required constraints.

By understanding the underlying logic and implementing the provided code, you can effectively count valid sequences for pickup and delivery orders, ensuring that each delivery follows its corresponding pickup.

7. Frequently Asked Questions

Q1: What is dynamic programming, and why is it useful in this context?

A: Dynamic programming is a technique that involves caching pre-computed results to eliminate redundant computations and optimize time complexity. In this context, dynamic programming helps efficiently count valid pickup and delivery sequences by breaking down the problem into smaller subproblems and using memoization to store computed values.

Q2: What are the constraints for this problem?

A: The constraints are as follows:

• 1 <= n <= 500
• Return result modulo 10^9 + 7
• Pickup must occur before its corresponding delivery.

Q3: How does the iterative approach differ from the recursive approach in dynamic programming?

A:In the iterative approach, we start with the base case and iteratively build solutions for larger subproblems, eventually solving the main problem. In contrast, the recursive approach starts with the main problem and recursively breaks it down into smaller subproblems until it reaches the base case.

Q4: Why is modulo 10^9 + 7 used in the code?

A: Modulo 10^9 + 7 is often used in competitive programming and coding challenges to ensure that the result remains within a reasonable range and avoids integer overflow issues. It’s a common practice to use this modulus for calculations in such scenarios.