Leetcode 135 Candy (Hard) Solution:Hey there, coding enthusiasts! Welcome back to another exciting coding session. Today’s problem is a treat—literally! We’re going to solve the “Candy” problem. Imagine you have a bunch of kids lined up, each with a rating assigned to them. Your task is to distribute candies to these kids following two simple rules:
- Every child must get at least one candy.
- A child with a higher rating should get more candies than their immediate neighbors.
Sounds like a piece of cake, right? But here’s the twist: you need to accomplish this with the fewest candies possible. Let’s dig into the mechanics of this problem and how to approach it.
Leet Code : Intersection of Two Linked ListsLeet Code – Java | Python | C++ | Dart | Easy Solution
Explaining using the Hand written Notes. with example:
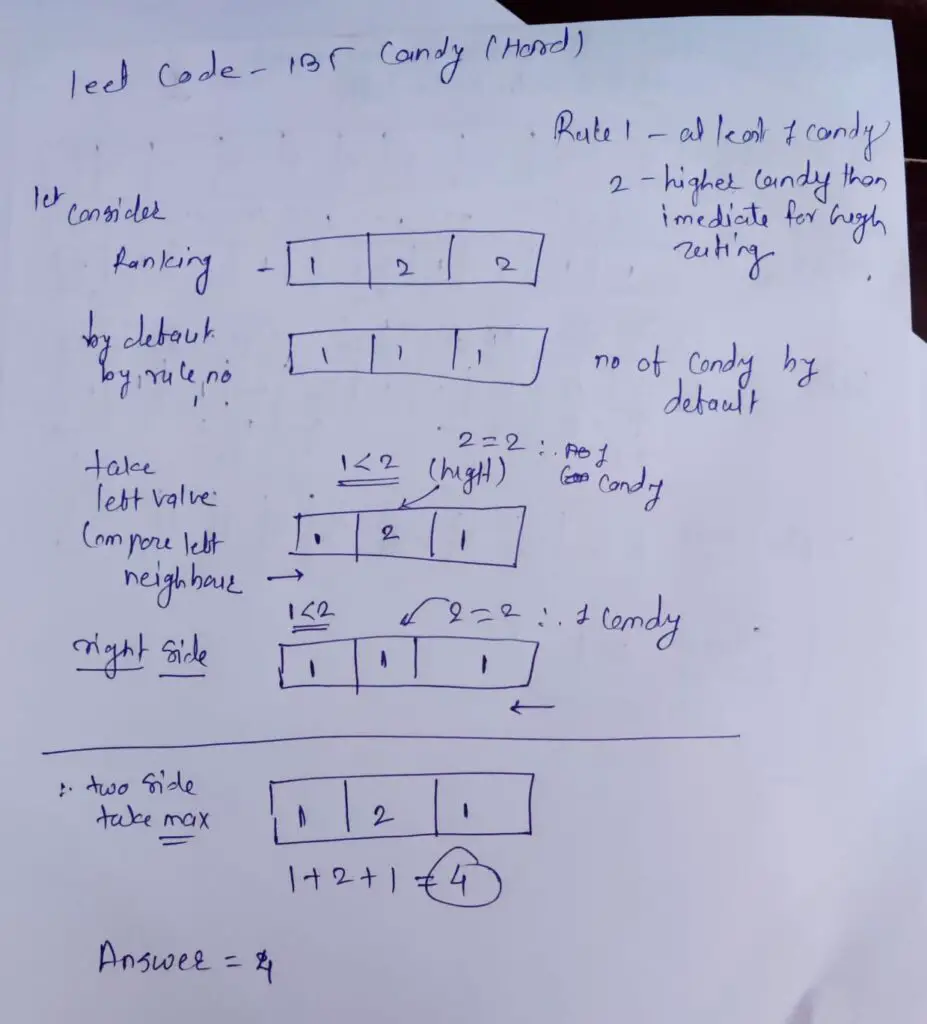
Also Read Maximum Width of a Binary Tree Leetcode
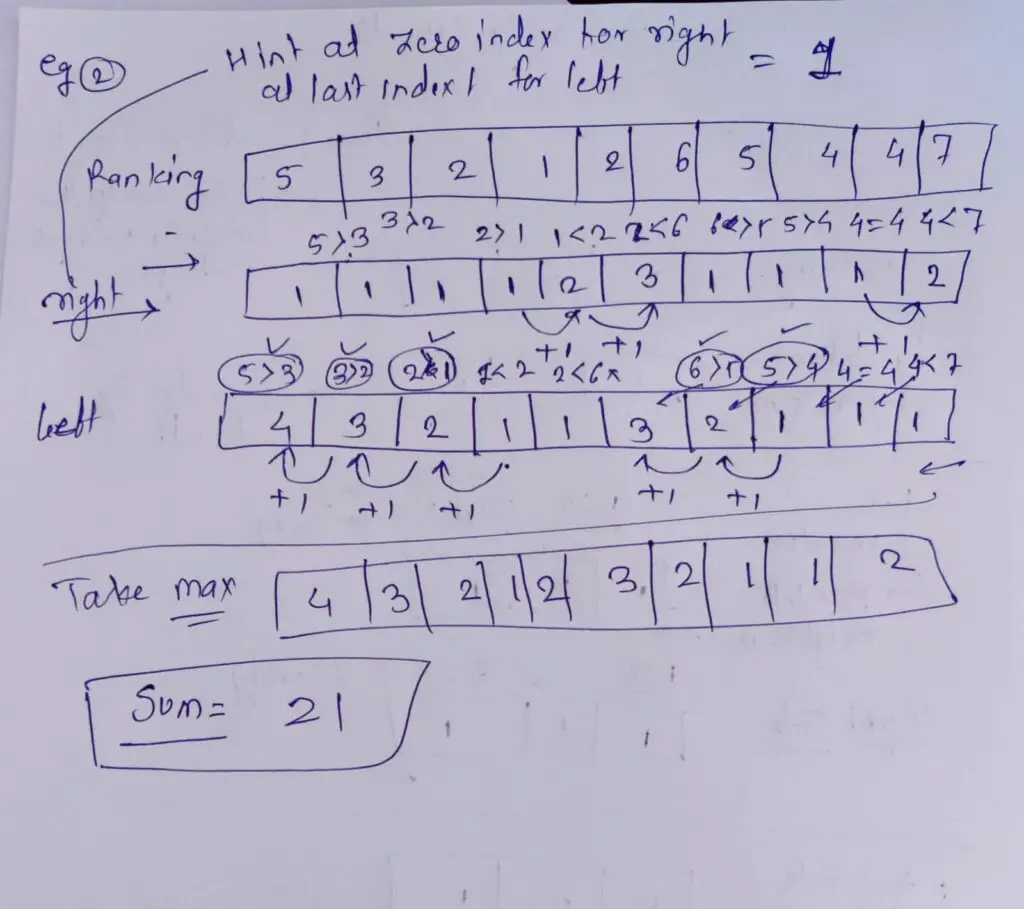
Read More : Leet Code 2612 Minimum Reverse Operations (Hard)
Strategies to Tackle the Problem
Greedy Algorithm: Two-Pass Method
Think of this as your candy distribution marathon. You’re taking two laps around the ratings track to make sure each child gets their candy fix while staying within the rules. 🏃♂️🍬🏁
One-Pass Greedy Algorithm: Up-Down-Peak Method
This one’s like Candy Math Olympics! Using a single pass, you juggle three variables – Up, Down, and Peak – to figure out how to be the candy hero efficiently. 🧮🍭🏆
Greedy Algorithm: Two-Pass Method Explained
What is a Greedy Algorithm?
A Greedy Algorithm makes choices that seem optimal at the moment. For this problem, we use a two-pass greedy approach to make sure each child gets the minimum number of candies that still satisfy the conditions.
The Nuts and Bolts of the Two-Pass Method
- Setting the Candy Stage: Start by whipping up a candies array, just as long as your ratings array. Give each child an initial treat score of 1. It’s like ensuring everyone at the candy party gets at least one candy, meeting the first condition.
- Forward March: Left to Right: Begin your candy adventure by strolling through the ratings array from the beginning to the end. For every child (except the very first one), compare their rating with the kid on their left. If it’s higher, add one more candy to the child on the right. It’s like giving the high-rater their due, but only compared to the neighbor on the left.
- Backward Roll: Right to Left: After your forward journey, it’s time to moonwalk back through the array, but this time, in reverse! Check each child’s rating against the one on their right. If it’s higher, make sure they’ve got more candies than their neighbor. Give them either their current candy count or one more than the right-side kid’s candies. This ensures everyone’s happy, satisfying both conditions.
- The Grand Candy Total: To wrap things up, add up all the candy scores in your candies array. Ta-da! That’s the magical minimum number of candies needed to make everyone smile, and you’ve just cracked the candy code! 🎉
Time and Space Complexity
- Time Complexity: O(n), because we make two passes through the array.
- Space Complexity: O(n), for storing the candies array.
Python
class Solution:
def candy(self, ratings: List[int]) -> int:
n = len(ratings)
candies = [1] * n
for i in range(1, n):
if ratings[i] > ratings[i-1]:
candies[i] = candies[i-1] + 1
for i in range(n-2, -1, -1):
if ratings[i] > ratings[i+1]:
candies[i] = max(candies[i], candies[i+1] + 1)
return sum(candies)Leet code :Zigzag Conversion solution c++ , Java , Python , JavaScript , Swift ,TypeScript
C++
#include <vector>
#include <algorithm>
class Solution {
public:
int candy(std::vector<int>& ratings) {
int n = ratings.size();
std::vector<int> candies(n, 1);
for (int i = 1; i < n; ++i) {
if (ratings[i] > ratings[i - 1]) {
candies[i] = candies[i - 1] + 1;
}
}
for (int i = n - 2; i >= 0; --i) {
if (ratings[i] > ratings[i + 1]) {
candies[i] = std::max(candies[i], candies[i + 1] + 1);
}
}
int totalCandies = 0;
for (int candy : candies) {
totalCandies += candy;
}
return totalCandies;
}
};
Java
import java.util.Arrays;
public class Solution {
public int candy(int[] ratings) {
int n = ratings.length;
int[] candies = new int[n];
Arrays.fill(candies, 1);
for (int i = 1; i < n; i++) {
if (ratings[i] > ratings[i - 1]) {
candies[i] = candies[i - 1] + 1;
}
}
for (int i = n - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candies[i] = Math.max(candies[i], candies[i + 1] + 1);
}
}
int totalCandies = 0;
for (int candy : candies) {
totalCandies += candy;
}
return totalCandies;
}
}
JavaScript
var candy = function(ratings) {
const n = ratings.length;
const candies = new Array(n).fill(1);
for (let i = 1; i < n; i++) {
if (ratings[i] > ratings[i - 1]) {
candies[i] = candies[i - 1] + 1;
}
}
for (let i = n - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candies[i] = Math.max(candies[i], candies[i + 1] + 1);
}
}
return candies.reduce((a, b) => a + b, 0);
};
Let’s explore the one-pass greedy algorithm, known as the Up-Down-Peak method, next.
One-Pass Greedy Algorithm: Up-Down-Peak Method
Why Up, Down, and Peak?
🔼 Up: Counting the Ascension
Up keeps a tally of children with rising ratings compared to the previous child. It’s your guide to knowing how many candies a child with a higher rating deserves.
🔽 Down: Tallying the Descent
Down keeps tabs on children with decreasing ratings from their predecessors. It’s your tool to decide how many candies a child with a lower rating should receive.
🏔️ Peak: Reaching the Summit
Peak stands sentinel at the highest point of an ascending sequence. When a descending sequence follows the peak, it’s your beacon to fine-tune candy distribution.
The Nuts and Bolts of the One-Pass Method
🚀 Initialization: Set the stage by initializing ret (our candy count) to 1 because every child deserves at least one candy. Initialize up, down, and peak, all starting at 0.
🔄 Ratings Rhapsody: As we traverse the ratings array, the variables come alive:
- 📈 If the rating rises: Increment up and peak by 1. Reset down to 0. Here, we add up + 1 to ret because the current child should enjoy one more candy than their predecessor. 🍭
- 📊 If ratings remain the same: Reset up, down, and peak to 0. Since there’s neither an ascent nor descent in this scenario, we simply add 1 to ret, ensuring each child gets at least one candy. 🍬
- 📉 If the rating descends: Increment down by 1 and say goodbye to up, resetting it to 0. Here, we add down to ret. But there’s a twist! If peak is greater than or equal to down, we subtract 1 from ret. This smart move acknowledges that the peak child can share the same number of candies as one of the children in the declining sequence, allowing us to reduce the total candy count. 🍫
Return the Total Candy Count
At the end of the loop, ret will contain the minimum total number of candies needed for all the children, so return ret.
By using up, down, and peak, we can efficiently traverse the ratings list just once, updating our total candies count (ret) as we go. This method is efficient and helps us solve the problem in a single pass, with a time complexity of O(n).
Also Read : Leet code 206 Reverse Linked List (EAZY)
Time and Space Complexity
- Time Complexity: O(n), for the single pass through the ratings array.
- Space Complexity: O(1), as we only use a few extra variables.
Python
class Solution:
def candy(self, ratings: List[int]) -> int:
if not ratings:
return 0
ret, up, down, peak = 1, 0, 0, 0
for prev, curr in zip(ratings[:-1], ratings[1:]):
if prev < curr:
up, down, peak = up + 1, 0, up + 1
ret += 1 + up
elif prev == curr:
up = down = peak = 0
ret += 1
else:
up, down = 0, down + 1
ret += 1 + down - int(peak >= down)
return retC++
#include <vector>
class Solution {
public:
int candy(std::vector<int>& ratings) {
if (ratings.empty()) {
return 0;
}
int ret = 1;
int up = 0;
int down = 0;
int peak = 0;
for (int i = 0; i < ratings.size() - 1; i++) {
int prev = ratings[i];
int curr = ratings[i + 1];
if (prev < curr) {
up++;
down = 0;
peak = up;
ret += 1 + up;
} else if (prev == curr) {
up = down = peak = 0;
ret += 1;
} else {
up = 0;
down++;
ret += 1 + down - (peak >= down ? 1 : 0);
}
}
return ret;
}
};
Java
public class Solution {
public int candy(int[] ratings) {
if (ratings.length == 0) {
return 0;
}
int ret = 1;
int up = 0;
int down = 0;
int peak = 0;
for (int i = 0; i < ratings.length - 1; i++) {
int prev = ratings[i];
int curr = ratings[i + 1];
if (prev < curr) {
up++;
down = 0;
peak = up;
ret += 1 + up;
} else if (prev == curr) {
up = down = peak = 0;
ret += 1;
} else {
up = 0;
down++;
ret += 1 + down - (peak >= down ? 1 : 0);
}
}
return ret;
}
}
JavaScript
var candy = function(ratings) {
if (ratings.length === 0) {
return 0;
}
let ret = 1;
let up = 0;
let down = 0;
let peak = 0;
for (let i = 0; i < ratings.length - 1; i++) {
const prev = ratings[i];
const curr = ratings[i + 1];
if (prev < curr) {
up++;
down = 0;
peak = up;
ret += 1 + up;
} else if (prev === curr) {
up = down = peak = 0;
ret += 1;
} else {
up = 0;
down++;
ret += 1 + down - (peak >= down ? 1 : 0);
}
}
return ret;
};
